Você Sabia - Você conhece o número mágico?

1089 é conhecido como o número mágico.
Veja porque:
Escolha qualquer número de três algarismos distintos: por exemplo, 875.
Agora escreva este número de trás para frente e subtraia o menor do maior:
875 - 578 = 297
Agora inverta também esse resultado e faça a soma:
297 + 792 = 1089  (o número mágico)

Você Sabia - Obtendo um quadrado perfeito

Você sabia que adicionando o número 1 à multiplicação de quatro números consecutivos você obtém um quadrado perfeito?
Exemplo: 1*2*3*4+1 = 25

Você Sabia - O maior número primo gêmeos conhecido.

 O maior par de primos gêmeos conhecido é 2003663613 . 2195000+/-1. Esses primos têm 58711 dígitos, e foram descobertos em janeiro de 2007. 

Trigonometria e Arquitetura

Não é possível separar a arquitetura da trigonometria, o que é fundamental para superfícies curvas em materiais de construção como aço e vidro. A ciência é utilizada para determinar a altura de prédios ou criar objetos dimensionais para utilizar em construções. A trigonometria é utilizada para fazer demarcações de cubículos em um prédio de escritórios, além de ser útil na predeterminação de padrões geométricos e da quantidade de material e mão-de-obra necessários para erguer uma estrutura. Quando ela estiver erguida, não só será forte, mas também terá medidas precisas.

Karina

Trigonometria na imagem digital

Imagem digital

A mesma ciência é utilizada na indústria musical. O som viaja em ondas que são utilizadas no desenvolvimento de música pelo computador. Um computador não entende a música como o ser humano; ele a representa matematicamente pelas suas ondas constituintes. Precisamente, engenheiros de som que trabalham no avanço da música digital e compositores de alta tecnologia precisam aplicar a lei básica da trigonometria, como as funções de seno e cosseno. Os padrões das ondas de música não são tão regulares como as das funções seno e cosseno, mas elas ainda são úteis no desenvolvimento da música digital.

Karina

Trigonometria na navegação, geografia e astronomia

A triangulação, que é a aplicação da trigonometria, é utilizada por astrônomos para calcular a distância entre a Terra e estrelas próximas. Em geografia, ela é utilizada para medir a distância entre pontos de referência, além de ser também utilizada em sistemas de navegação por satélite. Por exemplo, um piloto decolando do aeroporto de Guarulhos em São Paulo deverá saber qual o ângulo de decolagem e quando deve virar a um certo ângulo no céu para chegar até o aeroporto Heathrow em Londres.

Karina

Síntese do trimestre - Karina

Na minha síntese eu escolhi falar um pouco mais sobre o Teodolito e a Trigonometria.
Bom, no outro post eu citei que o Teodolito serve-nos como um instrumento de medição, o Teodolito, nada mais é que uma aplicação prática da Trigonometria.

"A trigonometria é uma área da matemática que prova a propriedade dos triângulos. Ela é usada em sistemas de satélites e astronomia, aviação, engenharia, levantamento topográfico, geografia e muitas outras áreas. Precisamente, a trigonometria é um ramo da matemática que lida com triângulos, círculos, ondas e oscilações."

Eu particularmente gostei bastante da trigonometria, achei super fácil os cálculos e consegui aprender bastante.

Minha síntese continua nos posts sobre astronomia, imagem digital, etc.

Gráficos no Excel

Na aula de matemática, no terceiro trimestre, trabalhamos com gráficos e para nosso auxílio, utilizamos a ferramenta Excel. O Excel é uma ferramenta magnífica que nos permite, também, a criar gráficos de diferentes modelos. O Excel, apesar de muitas pessoas o acharem um bicho de 7 cabeças, é bem prático e o mais interessante é que se você souber usar não terá tanto trabalho para fazer contas e não restará dúvidas se está ou não certo o gráfico. O sistema do Excel permite ter os resultados em mãos e contém varios estilos de gráficos dependendo de cada tipo de conta. Muitos utilizam esse programa para seus trabalhos no dia-a-dia!
Gostamos bastante de trabalhar com os gráficos no Excel e é interessante nós aprendermos a utilizar o mesmo, já que em várias profissões utilizamos o Excel.

Jogo - Trigonometria em Jogo de Bilhar

http://rived.mec.gov.br/atividades/matematica/mundo_trigonometria/aplicacoes/sinuca.html

Karina

Síntese do trimestre - Rafaella

Teorema de tales - Rafaella Garcia

Sobre o teorema:
Tales de Mileto foi um importante filósofo, astrônomo e matemático grego que viveu antes de Cristo. Ele usou seus conhecimentos sobre Geometria e proporcionalidade para determinar a altura de uma pirâmide. Em seus estudos, Tales observou que os raios solares que chegavam à Terra estavam na posição inclinada e eram paralelos, dessa forma, ele concluiu que havia uma proporcionalidade entre as medidas da sombra e da altura dos objetos.
O Teorema de Tales pode ser determinado pela seguinte lei de correspondência:

“Feixes de retas paralelas cortadas ou intersectadas por segmentos transversais formam segmentos de retas proporcionalmente correspondentes”.

Esse conteúdo, na minha visão, foi muito fácil e praticamente todos alunos da sala de aula conseguiram compreender bem. Ele não exigia muito, mas também nem tão pouco! Cada um tem sua visão do conteúdo e vários podem achar ele difícil na primeira vista, mas quando se aprende e se entende, tudo fica mais fácil. O Teorema de Tales é utilizado em diversas áreas.
ex: É possível descobrir o tamanho de um prédio apenas observando o ângulo que a sua sombra forma com o chão.

Teodolito caseiro

No dia 27/11 construímos um Teodolito na aula de matemática.
Para isso, utilizamos os seguintes materiais:
- Canudo
- Papelão
- Porca
- Fita métrica(Aplicação prática)
- Cordão
- Cola
- Transferidor de papel(Entregue pela professora)

1 Passo - Amarramos a porca no cordão.
2 Passo - Colamos o transferidor no papelão e o cortamos.
3 Passo - Furamos o ponto zero do transferidor e amarramos o cordão com a porca no mesmo.
4 Passo - Colamos o canudo na parte de cima do transferidor.
5 Passo - O Teodolito está pronto!

Aplicação Prática

No dia 29/11 realizamos a aplicação prática do Teodolito.

Mas para que serve o Teodolito?

Teodolito é um instrumento usado para medição. É geralmente usado para engenharia geológica. Esse aparelho consiste de um par de círculos graduados posicionados em ângulos retos entre si. O teodolito é usado principalmente para medidas de ângulos horizontais e verticais. Entretanto, esses instrumentos medem ângulos horizontais com maior precisão que ângulos verticais, uma vez que esta é a principal função nas medições.

Karina

História do Teodolito

História

Teodolitos existem há muito tempo, datados desde os alidades, dispositivo que providencia mapa geográfico do terreno. Ele consiste de uma mesa plana e um telescópio acoplado no topo do alidade, peça do equipamento caracterizada pela aparência de garfo. Em 1571, um livro de pesquisa chamado "Pantometria" providenciou a primeira descrição do teodolito, creditada a Thomas Digges, que também é associado à invenção do equipamento.

Jonathan Sisson construiu o primeiro teodolito contendo quatro parafusos niveladores, apesar de sua invenção ser atribuída a Ignácio Porro, inventor de instrumentos óticos, em 1835. Na verdade seu invento foi o taquímetro auto-redutor, um instrumento que possuía os mesmos elementos do teodolito, mas com um dispositivo ótico.Porro foi um dos inúmeros inventores que contribuíram para o aprimoramento do teodolito, cujo principio de funcionamento já era conhecido há muito.
Ao longo dos anos foi sendo transformado e a ele agregados sistemas e mecanismos que o tornaram mais preciso em suas medições.

O teodolito foi criado para substituir o Círculo de Borda - instrumento utilizado para medir com precisão ângulos horizontais e verticais que permitia medidas mais precisas entre as distâncias de um ponto a outro, da elevação e direção de determinado local.Círculo de Borda Brunner século XVIII.

O teodolito foi muito utilizado nas explorações do território brasileiro e demarcação de limites, como na demarcação do Planalto Central do Brasil, em 1892, e pela Comissão de Limites entre Brasil e Bolívia. O teodolito repetidor selecionado para compor o multimídia para a exposição de longa duração do museu foi doado ao Observatório Nacional em 1862 pelo Conde Prados e hoje faz parte do acervo do museu. Este instrumento foi utilizado pela Comissão de Pernambuco durante a Observação da Passagem de Vênus pelo disco solar, em 1882, e participou da Exposição Internacional do Centenário da Independência do Brasil, em 1922, realizada no Palácio dos Estados, no Rio de Janeiro.

Karina

Trigonometria

Trigonometria é bem legal e fácil. No início você acha que é a matéria mais difícil do ano, mas depois você repare que não é. A trigonometria (da 8ª serie) nós aprendemos o Cosseno, Seno e tangente. Como na imagem abaixo nós descobrimos os valores pela divisão:

Para entender melhor seno, cosseno e tangente.

Seno

Dado um triângulo retângulo, o seno de um dos seus 2 ângulos agudos é a proporção entre o comprimento do cateto oposto a este ângulo e o comprimento da hipotenusa, calculada, como toda proporção, pela divisão de um valor pelo outro, a referência da proporção.

No círculo trigonométrico, o seno de um ângulo qualquer pode ser visualizado na projeção do seu raio (por definição igual a 1) sobre o eixo vertical.

Cosseno

Dado um triângulo retângulo, o cosseno de um dos seus 2 ângulos agudos é a proporção entre o comprimento do cateto adjacente a este ângulo e o comprimento da hipotenusa, calculada, como toda proporção, pela divisão de um valor pelo outro, a referência da proporção.

Tangente

Dado um triângulo retângulo, a tangente de um dos seus 2 ângulos agudos é a proporção entre o comprimento do cateto oposto a este ângulo e o comprimento do cateto adjacente a ele, calculada, como toda proporção, pela divisão de um valor pelo outro, a referência da proporção.

Aplicação da Trigonometria.

Existem diversas aplicações da trigonometria e das funções trigonométricas. Por exemplo, a técnica da triangulação é usada em astronomia para estimar a distância das estrelas próximas; em geografia para estimar distâncias entre divisas e em sistemas de navegação por satélite. As funções seno e cosseno são fundamentais para a teoria das funções periódicas, as quais descrevem as ondas sonoras e luminosas.

Campos que fazem uso da trigonometria ou funções trigonométricas incluem astronomia (especialmente para localização de posições aparentes de objetos celestes, em qual a trigonometria esférica é essencial) e portanto navegação (nos oceanos, em aviões, e no espaço), teoria musical,acústica, óptica, análise de mercado, eletrônica, teoria da probabilidade, estatística, biologia, equipamentos médicos (por exemplo, Tomografia Computadorizada e Ultrassom), farmácia, química, teoria dos números (e portanto criptologia), sismologia, meteorologia, oceanografia, muitas das ciências físicas, solos (inspeção e geodesia), arquitetura, fonética, economia, engenharia, gráficos computadorizados, cartografia, cristalografia e desenvolvimento de jogos.

Alice Alves

Mestre e Adivinho

Jogo Mestre e Adivinho.

Esse jogo é um jogo bem fácil de se jogar e bem legal. Nele utilizamos a matemática (obvio) e a nossa adivinhação.

O jogo tem um tabela que é assim:

Para jogar você precisa ter um grupo de no máximo 4 pessoas. Cada um tem a sua vez de ser o mestre e o adivinho.

Quem é o adivinho, irá falar um número qualquer. O mestre irá escolher um frase, como por exemplo:

O dobro de número dito mais um.

Após escolher a frase ele irá fazer os cálculos com o número dito e irá dar a resposta para o adivinho. O adivinho com o resultado precisa adivinhar a frase do mestre.

O jogo é bem divertido e pode se fazer em casa, você só precisa criar umas frases e fazer a tabela.

Ps.: Ocorreu um pequeno problema com a imagem no blog e ele ficou assim, virada.

Apresentação

Somos um trio, Rafaella, Karina e Alice(14 anos) estamos na 8ª serie, turma 81 e estamos construindo este blogfólio para a avaliação da professora em relação aos trabalhos que nós fizemos e a dedicação que demos a eles. 

Nesses ano nossos objetivos na matemática e em geral, é obviamente, aprender e conseguir terminar o Ensino Fundamental sem preocupações no final do ano.

Simetria dos Polígonos

Esse exercício se chama “Simetria dos Polígonos”, foi bem fácil de fazer. No encarte do nosso livro de aula tinha essas figuras e em uma aula tivemos que “desenhar” as retas para mostrar quantas vezes cada figura tinha o tão famoso eixo de simetria. No encarte tinha: Octógono (8 lados), Eneágono (9 lados), hexágono (6 lados), triangulo (3 lados), quadrado (4 lados), heptágono (7 lados), decágono (10 lados) e pentágono (5 lados). 

Flor Convite

Nós elaboramos, em uma das nossas aulas de matemática, uma flor convite, para isso, precisávamos utilizar compasso e régua. Para muitos foi fácil e rápido, mas alguns tiveram dificuldade em faze-la. A flor convite foi um trabalho no qual nós vimos a relação de algo que pessoas fazem muitas vezes para festas (convites), ou ate mesmo uma carta fofa para alguém, e nisso também exige que utilizemos a matemática.

Curiosidade - Você sabe quanto vale um centilhão?

O maior número aceito no sistema de potências sucessivas de dez, é o centilhão, registrado pela primeira vez em 1852. Representa a centésima potência de um milhão, ou o número 1 seguido de 600 zeros (embora apenas utilizado na Grã-Bretanha e na Alemanha).

Curiosidade - Datas Históricas

Quarta-feira, dia 20 de fevereiro de 2002 foi uma data histórica. Durante um minuto, houve uma conjunção de números que somente ocorre duas vezes por milênio.

Essa conjugação ocorreu exatamente às 20 horas e 02 minutos de 20 de fevereiro do ano 2002, ou seja, 20:02 20/02 2002.

É uma simetria que na matemática é chamada de capicua (algarismos que dão o mesmo número quando lidos da esquerda para a direita, ou vice-versa). A raridade deve-se ao fato de que os três conjuntos de quatro algarismos são iguais (2002) e simétricos em si (20:02, 20/02 e 2002).

A última ocasião em que isso ocorreu foi às 11h11 de 11 de novembro do ano 1111, formando a data 11h11 11/11/1111. A próxima vez será somente às 21h12 de 21 de dezembro de 2112 (21h12 21/12/2112). Provavelmente não estaremos aqui para presenciar. 

Depois, nunca mais haverá outra capicua. Em 30 de março de 3003 não ocorrerá essa coincidência matemática, já que não existe a hora 30.

DONALD NO PAIS DA MATEMÁGICA

Em sala de aula, nós vimos um tipo de filmezinho da Disney. Se chama DONALD NO PAIS DA MATEMÁGICA. É bem legal e ele nos mostra principalmente sobre geometria. Uma das partes mais importantes do “filme” é quando eles começam a explicar sobre a beleza áurea. Abaixo tem o link do vídeo. Recomendo, é bem interessante, principalmente quem gosta de aprender sobre curiosidades da matemática.

http://www.youtube.com/watch?v=TphWfs_OXkU

Curiosidade - Você sabe o que são números pitagóricos?

São os inteiros que cumprem a equação de Pitágoras a2 + b2 = c2 . Por exemplo: 3, 4 e 5.

Curiosidade - Você sabe o que são números amigáveis?

Números amigáveis são pares de números onde um deles é a soma dos divisores do outro.

Por exemplo, os divisores de 220 são 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 e 110, cuja soma é 284.

Por outro lado, os divisores de 284 são 1, 2, 4, 71 e 142 e a soma deles é 220. Fermat descobriu também o par 17.296 e 18.416. Descartes descobriu o par 9.363.584 e 9.437.056.

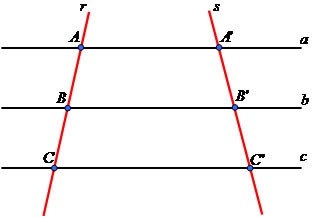
Teorema de Tales - Demonstração, Relação e Escalas

O teorema de tales:

Tales de Mileto foi um importante filósofo, astrônomo e matemático grego que viveu antes de Cristo. Ele usou seus conhecimentos sobre Geometria e proporcionalidade para determinar a altura de uma pirâmide. Em seus estudos, Tales observou que os raios solares que chegavam à Terra estavam na posição inclinada e eram paralelos, dessa forma, ele concluiu que havia uma proporcionalidade entre as medidas da sombra e da altura dos objetos

Demonstração:

Se B’C’ é paralelo a BC, então os triângulos B’C'B e B’C'C tem mesma área porque possuem mesma base B’C’ e alturas relativas a essa base também iguais. Acrescentando a esses triângulos o triângulo AB’C', concluímos que os triângulos ABC’ e AB’C também possuem mesma área. Se dois triângulos possuem mesma altura ( h1 é altura relativa à base AB’ do triângulo AB’C’ e relativa à base AB  do triângulo ABC’ ; h2 é altura relativa à base AC do triângulo AB’C e relativa à base AC’ do triângulo AB’C'), então a razão entre suas áreas é igual à razão entre suas bases, logo,
AB’/AB = Área (AB’C')/ Área(ABC’) = Área(AB’C')/Área ( AB’C) = AC’/AC o que prova o teorema.

Relação entre a semelhança e o teorema de Tales:

O Teorema de Tales possui diversas aplicações no cotidiano, constituindo uma importante ferramenta da Geometria no cálculo de distâncias inacessíveis e nas relações envolvendo semelhança entre triângulos. A melhor forma de visualizar as aplicabilidades do Teorema proposto por Tales de Mileto é através de alguns exemplos. 

Exemplo 1 

Calcule o comprimento da ponte que deverá ser construída sobre o rio, de acordo com o esquema a seguir.

De acordo com a figura temos um triângulo ABC e o segmento DE dividindo o triângulo, sendo formado o triângulo ADE. As informações que temos são as medidas dos seguintes segmentos: AD = 10m, AE = 9m, EC = 18m e DB = x. O valor de DB será determinado através do Teorema de Tales que diz: “retas paralelas cortadas por transversais formam segmentos proporcionais.” Desse modo, podemos estabelecer a seguinte relação:

Portanto, a ponte terá 20 metros de comprimento. 

Relação entre a semelhança e a escala:

ESCALAS GRÁFICAS: A escala gráfica é representada sob a forma de um segmento de recta, normalmente subdividido em secções e ao longo do qual são registadas as distâncias reais correspondentes às dimensões do segmento. Nalguns mapas essas distâncias surgem na escala métrica europeia ( fig. 1) e noutros conjugam-se as unidades de medida europeias com as anglo-saxónicas (fig. 2) - em milhas ( utilizadas pelos ingleses e americanos). ESCALAS GRÁFICAS: A escala gráfica é representada sob a forma de um segmento de recta, normalmente subdividido em secções e ao longo do qual são registadas as distâncias reais correspondentes às dimensões do segmento. Nalguns mapas essas distâncias surgem na escala métrica europeia ( fig. 1) e noutros conjugam-se as unidades de medida europeias com as anglo-saxónicas (fig. 2) - em milhas ( utilizadas pelos ingleses e americanos).

 Fig. 1 - Escala gráfica em Km ( escala métrica)                     Fig. 2 - Escala gráfica em Km e milhas

Polígonos Inscritos

Um polígono está inscrito numa circunferência se todos os seus vértices são pontos da circunferência. Essa circunferência diz-se circunscrita ao polígono.

Os polígonos regulares podem sempre ser inscritos numa circunferência, o mesmo não acontecendo com os polígonos não regulares. Os triângulos são uma excepção a este facto, pois qualquer triângulo pode ser inscrito numa circunferência. Relativamente aos quadriláteros, tal só se verifica se a soma dos seus ângulos internos opostos for 180º.

Estas duas últimas afirmações podem ser verificadas nas seguintes imagens: (triângulo e quadrilátero)

Beleza Áurea

Foi Marcos Vitrúvio Polião, arquiteto e engenheiro romano que viveu no século I a.C. quem primeiro concebeu a idéia da Proporção Áurea.

Denotada pela letra grega φ (phi) e com o valor arredondado a três casas decimais de 1,618, este é chamado o número da perfeição, freqüente em pinturas renascentistas. Leonardo da Vinci representou a descoberta de Vitrúvio em seu famoso desenho intitulado Homem Vitrúvio.

A Proporção Áurea está envolvida com a natureza do crescimento. Phi pode ser encontrado na proporção das conchas, seres humanos (o tamanho das falanges, ossos dos dedos, por exemplo), até na relação dos machos e fêmeas de qualquer colméia do mundo, e em inúmeros outros exemplos que envolvem a ordem do crescimento. 

O fato de ser encontrado através de desenvolvimento matemático é que o torna fascinante.

Na aula fizemos um trabalho sobre a beleza Áurea, nos medindo e vendo quem chega mais perto de 1,6. Foi bem divertido.

Jogo Descobrindo a Senha

No livro havia uma proposta de jogo que envolvia probabilidade e problemas de contagem, esse jogo se chama Descobrindo a Senha. O jogo era, resumidamente, tentar descobrir a senha que seu colega tivesse escrito no papel, as letras da senha teriam que ser A, B, C e D. Por exemplo, o desafiante escreve CDBA, e o desafiado teria que acertar esta senha. Nós gostamos bastante do jogo, ele é divertido e nos ajudou a trabalhar mais tanto a probabilidade, quanto os problemas de contagem.

Mosaico

Definição

Se você procurar um dicionário, ele vai lhe dizer qua a palavra MOSAICO significa dar forma ou arranjar pequenos quadrados em padrão de ladrilhagem.

As primeiras ladrilhagens foram feitas com ladrilhos quadrados.

Um polígono regular tem 3 ou 4 ou 5 ou mais lados e ângulos, todos iguais. Um mosaico regular significa um mosaico composto de polígonos regulares congruentes.

Apenas três polígonos regulares são usados no plano euclideano: triângulos, quadrados ou hexágonos. Nós não podemos mostrar o plano inteiro, mas imagine que estes são pedaços tirados de um plano que foi ladrilhado. Estão aqui os exemplos de

um mosaico de triângulos
um mosaico de quadrados
um mosaico de hexágonos

Quando você olha estes três exemplos você pode fácilmente observar que os quadrados estão alinhados uns com os outros, enquanto os triângulos e os hexágonos não. Também, se você olhar 6 triângulos de cada vez, eles formam um hexágono, assim a ladrilhagem dos triângulos e a ladrilhagem dos hexágonos são similares e não pode ser formadas alinhando os ladrilhos com uma translação.

Você pode medir os ângulos internos de cada um destes polígonos:

Polígono triângulo quadrado pentagon hexágono mais de seis lados

Medida do ângulo em graus 60 90 108 120 mais de 120 graus

Desde que os polígonos regulares em um ladrilhagem devem encher o plano em cada vértice, o ângulo interno deve ser um divisor exato de 360 graus. Isto é verdade para o triângulo, o quadrado, e o hexágono, e você pode construir ladrilhagens trabalhando com estas figuras. Para todos os outros, os ângulos internos não são divisores exatos de 360 graus, e conseqüentemente aquelas figuras não podem ladrilhar o plano.

Fonte: http://homes.dcc.ufba.br/~frieda/pedagogiadeprojetos/conteudos/mosaicopronto/oquee.htm

Acima está um dos mosaicos feitos em aula.

Museu da PUC

No dia 16/08 a 8ª série foi ao museu da PUC, cujo museu há muitos experimentos ligados á matemática, tanto é que existe um espaço reservado APENAS para a matemática. Lá vimos diversos assuntos que já estudamos, como por exemplo: Pitágoras e o teorema, simetria, poliedros regulares, etc.

 Nas fotos abaixo podemos observar alguns jogos que tinham no museu.

Na foto abaixo, podemos ver alguns Sólidos geométricos. 

Entre outros...

Tales de Mileto

Quem foi Tales de Mileto? Em que época ele viveu?

Tales de Mileto foi o primeiro matemático grego, nascido por volta do ano 640 e falecido em 550 a.c., em Mileto, cidade da Ásia Menor, descendente de uma família oriunda da Fenícia ou Beócia.

Quais foram os principais trabalhos dele?

Tales foi o primeiro a explicar o eclipse solar, ao verificar que a Lua é iluminada por esse astro.
Tales foi o primeiro a observar que o alimento de todas as coisas é úmido e que o próprio calor é gerado e alimentado pela umidade. Ora, aquilo de que se originam todas as coisas é o princípio delas. Daí lhe veio essa opinião, e também a de que as sementes de todas as coisas são naturalmente úmidas e de ter origem na água a natureza das coisas úmidas”.

Em matemática qual é o teorema que leva o seu nome? E o que diz o teorema?

Teorema de tales. O Teorema de Tales é determinado pela intersecção entre retas paralelas e transversais, que formam segmentos proporcionais. Foi estabelecido por Tales de Mileto, que defendia a tese de que os raios solares que chegavam à Terra estavam na posição inclinados. Partindo desse princípio básico observado na natureza, intitulou uma situação de proporcionalidade que relaciona as retas paralelas e as transversais.

Abaixo uma imagem representando o teorema:

Como ele fez para realizar a medição da pirâmide de Quéops?

Há duas versões para este fato. Hicrônimos, discípulo de Aristóteles, diz que Tales mediu o comprimento da sombra da pirâmide no momento em que nossas sombras são iguais a nossa altura, assim medindo a altura da pirâmide. A de Plutarco diz que fincando uma vara vertical no extremo da sombra projetada pela pirâmide, construímos à sombra projetada da vara, formando no solo dois triângulos semelhantes. 

PATequation

Esse é um site chamado PATequation, ele é bem interessante porque nos ajuda a estudar equações, aponta nossos erros e nos ajuda e entender melhor as equações de 2ª grau. Vale a pena entrar e conferir!

Poliedros no dia-a-dia

Poliedros de palitos

Essa atividade foi muito interessante porque criamos uma forma geométrica em 3D chamada octaedro. Foi bem diferente e uma atividade onde podemos interagir com os outros alunos ao invés de ficar sentada na sala de aula desenhando uma forma. Essa foto é da fase de colagem, onde nós colamos os palitinhos de churrascos já pintados.

Agora olhe como ficou lindo:

 E também teve os outros grupos que fizeram outras forma: