Tales de Mileto

Quem foi Tales de Mileto? Em que época ele viveu?

Tales de Mileto foi o primeiro matemático grego, nascido por volta do ano 640 e falecido em 550 a.c., em Mileto, cidade da Ásia Menor, descendente de uma família oriunda da Fenícia ou Beócia.

Quais foram os principais trabalhos dele?

Tales foi o primeiro a explicar o eclipse solar, ao verificar que a Lua é iluminada por esse astro.
Tales foi o primeiro a observar que o alimento de todas as coisas é úmido e que o próprio calor é gerado e alimentado pela umidade. Ora, aquilo de que se originam todas as coisas é o princípio delas. Daí lhe veio essa opinião, e também a de que as sementes de todas as coisas são naturalmente úmidas e de ter origem na água a natureza das coisas úmidas”.

Em matemática qual é o teorema que leva o seu nome? E o que diz o teorema?

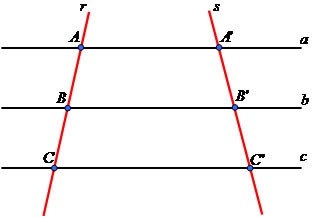
Teorema de tales. O Teorema de Tales é determinado pela intersecção entre retas paralelas e transversais, que formam segmentos proporcionais. Foi estabelecido por Tales de Mileto, que defendia a tese de que os raios solares que chegavam à Terra estavam na posição inclinados. Partindo desse princípio básico observado na natureza, intitulou uma situação de proporcionalidade que relaciona as retas paralelas e as transversais.

Abaixo uma imagem representando o teorema:

Como ele fez para realizar a medição da pirâmide de Quéops?

Há duas versões para este fato. Hicrônimos, discípulo de Aristóteles, diz que Tales mediu o comprimento da sombra da pirâmide no momento em que nossas sombras são iguais a nossa altura, assim medindo a altura da pirâmide. A de Plutarco diz que fincando uma vara vertical no extremo da sombra projetada pela pirâmide, construímos à sombra projetada da vara, formando no solo dois triângulos semelhantes.